| Table of Contents |
Given cluster trees 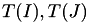 for the index sets
for the index sets 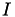 and
and 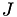 , the product index set
, the product index set 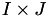 is to be partitioned. The trivial product of both cluster trees would yield a tree with
is to be partitioned. The trivial product of both cluster trees would yield a tree with 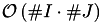 nodes, obviously exceeding the desired complexity. The restriction of the full product tree to those nodes, interesting for 𝓗-computations is performed by identifying admissibly blockes which are not refined, and for which the sub tree is eliminated from the product tree. For this identifcation the admissibility condition is used.
nodes, obviously exceeding the desired complexity. The restriction of the full product tree to those nodes, interesting for 𝓗-computations is performed by identifying admissibly blockes which are not refined, and for which the sub tree is eliminated from the product tree. For this identifcation the admissibility condition is used.
Admissibility Condition
Geometrical Case
Assuming appropriate properties of the operator that should be represented by 𝓗-matrices, the standard definition of admissibility uses diameters and distances between individual clusters. These terms have the standard definition in the geometrical case, e.g. the diameter of a cluster is the diameter of the bounding box or of the bounding sphere enclosing all indices and the distance is defined accordingly. Here, the standard admissibility condition is
![\[ \max\left( \mathnormal{diam}(s), \mathnormal{diam}(t) \right) \le \eta \cdot \mathnormal{dist}(s,t) \]](form_229.png)
which can usually be relaxed to
![\[ \min\left( \mathnormal{diam}(s), \mathnormal{diam}(t) \right) \le \eta \cdot \mathnormal{dist}(s,t) \]](form_230.png)
The parameter 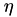 controls the ratio between the diameter and the distance, yielding a finer 𝓗-structure when
controls the ratio between the diameter and the distance, yielding a finer 𝓗-structure when 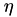 tends to 0. By default
tends to 0. By default 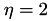 holds.
holds.
The implementation for the standard admissibility can be found in TStdAdmCond.
The boolean parameter defines the usage of 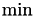 or
or 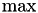 in the above admissibility condition and defaults to
in the above admissibility condition and defaults to 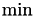 , e.g. the parameter is
, e.g. the parameter is false.
If a periodicity was set for the coordinates, this must also be set for the admissibility. Otherwise, the distance between clusters is computed without this periodicity:
High Frequency Case
For oscillating operators, e.g. Helmholtz or Maxwell, the rank of low-rank blocks in 𝓗-matrices will grow linearlly with the wave number. For large wave numbers and large blocks, this will easilly lead to a very high rank and therefore significant memory usage and computation times.
Due to this property, standard 𝓗-matrices are not capable of handling high frequency cases efficiently. However, in practise many problems may still be computed using 𝓗-matrices. 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 provides a modified admissibility condition (THiLoFreqGeomAdmCond), which limits the number of wave lengths per geometrical cluster and thereby also limits the rank:
Here, kappa denotes the wave number and nwaves defines the maximal number of wave lengths per cluster. In the low frequency case, the standard admissibility is applied, using the provided parameter eta.
Algebraic Case
In the case of algebraic clustering, the above definitions of the admissibility condition can also be used, if corresponding definitions for the diameter and the distance of clusters are available. Since in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈, algebraic clustering is based on graphs, both terms are defined in terms of path lengths. This leads to the implementation in TStdAlgAdmCond. It uses the sparse matrix for graph definition and furthermore, needs the mappings between internal and external ordering to correctly identify the indices:
The first parameter is again the 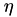 from the definition of the admissibility condition.
from the definition of the admissibility condition.
Unfortunately, computing distances and diameters in graphs is costly. Since in algebraic clustering the correspondence between real spatial coordinates and the nodes in graphs is only an approximation, the admissibility condition may be further relaxed, leading to the weak algebraic admissibility. Here, a block cluster is admissible, if no edge connects the two corresponding sub graphs. 𝓗-matrices defined by this admissibility condition usually have similar approximation and complexity properties as in the standard admissibility case, but the test can be done much more efficiently. The implementation of this admissbility condition can be found in TWeakAlgAdmCond, which again needs the matrix and the mappings for the admissibility test.
Construction
The construction of the block cluster tree is generic, once the admissibility condition is defined and implemented in TBCBuilder:
Objects of type TBlockClusterTree will not only store the actual tree but also the mappings between internal and external ordering supplied by the corresponding row and column cluster trees. In contrast to this a TBlockCluster object only represents the tree without any mappings. To access this tree from a TBlockClusterTree object, the root method is available, e.g.:
 1.8.9.1
1.8.9.1