| Table of Contents |
Unsymmetric Matrices
For unsymmetric matrices, 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 implements LU and LDU factorisation, i.e. the matrix 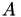 is factorised into
is factorised into
![\[ A = LU \quad \textnormal{or} \quad A = LDU \]](form_169.png)
with a lower triangular, unit diagonal matrix 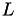 , a upper triangular matrix
, a upper triangular matrix 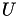 and, in the case of LDU a diagonal matrix
and, in the case of LDU a diagonal matrix 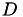 (in which case
(in which case 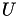 is also unit diagonal).
is also unit diagonal).
Both matrix factorisation are available in two modes:
- block-wise: the matrix factorisation is performed up to leaf matrices in the matrix hierarchy, e.g. dense diagonal matrices are not factorised but inverted.
- point-wise: a real LU (LDU) factorisation is computed, i.e. also dense diagonal blocks are factorised.
In the case of point-wise factorisation, the possibility of a break-down is high because pivoting is only possible to a very small degree for 𝓗-matrices and therefore not implemented in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈. Therefore, block-wise factorisation is the default factorisation mode, since it can only break down in the case of singular diagonal blocks (in which case some remedy is avaibable, see below).
The factorisation methods are implemented in the classes TLU and TLDU. Factorising 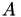 using default parameters can be performed as
using default parameters can be performed as
Here, a block-wise accuracy of 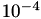 were used during LU. By replacing TLU with TLDU, the corresponding factorisation method is used. Furthermore, for both variants, functional forms are available, called lu and ldu:
were used during LU. By replacing TLU with TLDU, the corresponding factorisation method is used. Furthermore, for both variants, functional forms are available, called lu and ldu:
LU-Factor Evaluation: Linear Operators
Matrix factorisation is performed in place, i.e. the individual factors are stored within 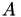 , thereby overwriting the original content. That also means, that
, thereby overwriting the original content. That also means, that 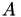 can no longer be used as a standard matrix object, e.g. for matrix vector multiplication, since for that, the content needs special interpretation, e.g. first multiply with upper triangular part, then with lower triangular.
can no longer be used as a standard matrix object, e.g. for matrix vector multiplication, since for that, the content needs special interpretation, e.g. first multiply with upper triangular part, then with lower triangular.
Special classes are avaiable in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 to perform such interpretation, namely:
- TLUMatrix, TLDUMatrix: compute matrix vector product
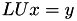 and
and 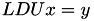 respectively,
respectively, - TLUInvMatrix, TLDUInvMatrix: compute matrix vector product
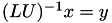 and
and 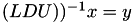 respectively.
respectively.
Since the corresponding objects do not provide standard matrix functionality, they are representatives of the linear operator class TLinearOperator. Linear operators only provide evaluation of the matrix-vector product, which itself is a limited version of the standard TMatrix matrix-vector multiplication since only updates of the destination vector are possible, e.g. either
![\[ y = A \cdot x \]](form_178.png)
or
![\[ y = y + \alpha A \cdot x \]](form_179.png)
However, also the transposed or hermitian evaluation are supported.
TLUMatrix (TLDUMatrix) and TLUInvMatrix (TLDUInvMatrix) objects may be created explicitely or by using the corresponding functions of TLU (TLDU):
- Remarks
- Since the "*Inv*" classes provide evaluation of the inverse, they can be used for preconditioning while solving equation systems iteratively (see ???).
Factorisation Parameters
So far, matrix factorisation was performed with default parameters. Options for matrix factorisation are provided in the form of a fac_options_t object. With it, you may select point-wise factorisation, e.g.:
Also, a progress meter may be assigned for the factorisation:
Furthermore, special modifications in case of a factorisation failure, e.g. for a singular matrix or for a matrix with a bad condition, may be activated.
- add_identity: replace
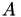 by
by 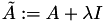 , with
, with 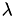 being chosen in some interval
being chosen in some interval ![$ [\lambda_0,\lambda_1] $](form_182.png) until
until 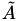 can be factorised,
can be factorised, - add_random: replace
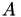 by
by 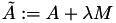 , with a random matrix
, with a random matrix 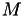 and
and 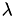 as in the previous case,
as in the previous case, - add_random_lr: replace
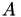 by
by 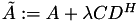 , with a random low-rank matrices
, with a random low-rank matrices 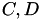 with increasing rank until a successfull factorisation can be computed (
with increasing rank until a successfull factorisation can be computed ( 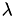 as before),
as before), - fix_cond: if
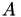 has a very high condition, its singular values
has a very high condition, its singular values 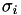 will be shifted by
will be shifted by 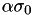 , e.g. the largest singular value.
, e.g. the largest singular value.
The first three modification techniques are exclusive, i.e. may not be combined, whereas the last method can be used parallel to the others. Furthermore, all modifications only apply to dense diagonal blocks, thereby bounding the computation complexity of all methods such that the overhead can be neglected.
- Remarks
- In most applications, using
add_identity(combined withfix_cond) is best for handling errors during factorisation.
Symmetric/Hermitian Matrices
If 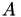 is symmetric (
is symmetric ( 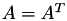 ) or hermitian (
) or hermitian ( 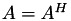 ), 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 provides the Cholesky (LL) and the LDL factorisation. These are implemented in the classes TLL and TLDL:
), 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 provides the Cholesky (LL) and the LDL factorisation. These are implemented in the classes TLL and TLDL:
or available in functional form:
- Remarks
- Please note, that TLU and TLDU will not work for symmetric/hermitian matrices as only the lower triangular part is stored and therefore, will throw an exception if called with such a matrix.
Evaluation of a factorised  is provided by TLLMatrix and TLDLMatrix, whereas evaluation of
is provided by TLLMatrix and TLDLMatrix, whereas evaluation of 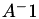 is implemented in TLLInvMatrix and TLDLInvMatrix. Please note, that the matrix format, e.g. whether symmetric or hermitian, is lost during factorisation but crucial for matrix evaluation and therefore, has to be provided while constructing these matrix objects:
is implemented in TLLInvMatrix and TLDLInvMatrix. Please note, that the matrix format, e.g. whether symmetric or hermitian, is lost during factorisation but crucial for matrix evaluation and therefore, has to be provided while constructing these matrix objects:
TLDL uses block-wise factorisation but can be switched to point-wise mode using fac_options_t objects as described above. Also, factorisation modifications/stabilisations may be activated for LDL factorisation. Neither of these is supported for Cholesky factorisation as this always used point-wise mode (block-wise is not possible). It is therefore not as stable as LDL factorisation.
Simplified Factorisation
Instead of chosing the factorisation technique by yourself and handling the creation of the corresponding linear operators, this can be simplified by using the functions factorise and factorise_inv:
This works for unsymmetric and symmetric/hermitian matrices. Furthermore, options to the factorisation may be provided as an additional argument.
 1.8.6
1.8.6