| Table of contents |
Given a sparse matrix 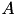 and a right hand hand side
and a right hand hand side 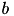 , the solution
, the solution 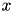 of
of
![\[Ax = b\]](form_80.png)
is sought, whereby 𝓗-LU factorisation shall be used to improve the convergence of an iterative solver. No geometrical data is assumed and hence, algebraic clustering is performed for converting 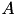 into an 𝓗-matrix. Furthermore, nested dissection is applied to improve the efficiency of the 𝓗-LU factorisation.
into an 𝓗-matrix. Furthermore, nested dissection is applied to improve the efficiency of the 𝓗-LU factorisation.
Loading the Sparse Matrix
The program starts with the inclusion of the needed header files and the initialisation of 𝓗𝖫𝖨𝖡𝗉𝗋𝗈.
The next step is the definition of the sparse matrix, which shall be read from a file. 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 supports various foreign matrix formats, e.g. Matlab, SAMG, Harwell-Boeing or Matrixmarket. In this example, the matrix is stored in Matlab format:
The class TAutoMatrixIO performs autodetection of the file format and is therefore suited for all supported formats.
- Remarks
- In the case of Matlab, TAutoMatrixIO reads in the first matrix found in the file. If you have stored several matrices in one file, you have to use TMatlabMatrixIO and provide the name of the matrix to read.
By using autoptr, the corresponding object is automatically deleted when the current block is left, thereby reducing the danger of memory leaks. This technique is extensively used in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈.
Since any kind of matrix may be stored in the given file, e.g. a dense matrix, but in the following sparse matrices are expected, the type of the matrix is tested:
The macro IS_TYPE returns true, if the corresponding object is of the given type. This is an example of the runtime type information system (RTTI) in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 and works similar to dynamic casts in C++. The advantage of the 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 RTTI is, that further information can be gathered, e.g. the type name through the function typestr(), independent of the corresponding C++ compiler support.
- Remarks
- The 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 RTTI is also faster than the C++ RTTI since only some numbers are compared but of course, the C++ approach is much more general and needs no special support by the programmer.
Finally, since we know by now that M contains a sparse matrix, we cast the pointer for easier use in the following. The macro ptrcast is just an abbreviation of a C++ cast and was introduced in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 for ease of use and for debugging purposes (ptrcast is different depending on compilation options).
We now make use of the TSparseMatrix pointer S and may output some information about it:
This includes the dimension of the matrix, i.e. the number of rows and columns, as well as the number of non zero elements. Furthermore, the value type, real of complex, and matrix properties are printed. Finally, the storage size and the Frobenius norm is computed.
Conversion to 𝓗-Format
Having a right hand side, the equation system above could now be solved using an iterative scheme. Unfortunately, most sparse matrices need some form of preconditioning for an acceptable convergence behaviour. The preconditioner shall be in the form of a 𝓗-LU factorisation of 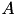 and hence, of
and hence, of S. For this, we need a cluster tree and a block cluster tree.
Since, by assumption, no geometrical data is available, the clustering is performed purely algebraically by using the connectivity relation of the indices stored in the sparse matrix itself. Furthermore, nested dissection is to be used, which needs some special clustering.
Algebraic clustering uses graph partitioning as the underlying technique. 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 implements two graph partitioning algorithms (TBFSAlgPartStart and TMLAlgPartStrat) and supports external algorithms, e.g. METIS and Scotch. Here we use the multi-level partitioning strategy implemented by TMLAlgPartStrat.
Nested dissection clustering is based on a standard bissection clustering algorithm, which therefore has to be defined explicitly in the form of TAlgCTBuilder, which on the other hand uses the graph partitioning strategy. Finally, TNDAlgCTBuilder computes the cluster tree for the index set defined by S:
Having the cluster tree, the block cluster tree can be computed:
Here, the weak admissibility condition for graphs, implemented by TWeakAlgAdmCond, is used. Since the block clusters to test are based on the internal ordering of the 𝓗-matrix but the sparse matrix is defined in the external ordering, the corresponding mappings between both is needed by the admissibility condition.
The printed sparsity constant gives some hint about the complexity of the 𝓗-matrix constructed over the block cluster tree, the smaller, the better.
The final conversion of the sparse matrix into 𝓗-format is performed by TSparseMBuilder. Here, again the mappings between internal and external ordering are needed. The accuracy can be usually neglected, since low rank blocks are usually empty (clusters of positive distance usually have no overlapping basis functions).
Matrix construction may use multiple threads, so the first argument to the build function is corresponding number to use. The mach_info object holds some information about the machine, e.g. number of available processors.
After matrix construction, the size of the 𝓗-matrix 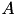 and its norm is printed together with the (relative) norm of the difference
and its norm is printed together with the (relative) norm of the difference 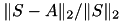 , indicating any approximation error.
, indicating any approximation error.
𝓗-LU factorisation
The factorisation of A may be computed differently, depending on the format of A, e.g. if it is symmetric or not. In the latter case the standard 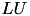 factorisation is used, implemented in TLU, while in the symmetric case the
factorisation is used, implemented in TLU, while in the symmetric case the 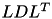 (or
(or 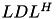 for hermitian matrices) factorisation implemented in TLDL is computed.
for hermitian matrices) factorisation implemented in TLDL is computed.
The factorisation is performed in place, i.e. the data of A is overwritten by the corresponding factores. This implies, that A is actually not a matrix object after the factorisation since the stored data depends on special handling. For this, inverse factorisation matrices are used which are available for each factorisation algorithm.
Some properties of the factorisation are printed next, most notably the inversion error 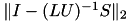 and the condition estimate
and the condition estimate 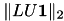 :
:
Solving the Equation System
Finally, the equation system can be solved using the inverse of the matrix factorisation as a preconditioner. The right hand side is assumed to be available in Matlab format and is read in using TAutoVectorIO, which again performs file format auto detection. The solution vector is created using the col_vector function of S, which returns a vector defined over the column index set of S.
The TAutoVectorIO class can also be used to write the solution vector to a file, again in Matlab format.
- Remarks
- File format autodetection when reading a file is performed by actually looking at the content of the file, yielding a robust autodetection algorithm. When writing a file, only the filename, especially the filename extension is used, which may not unique between different formats (but works in most cases).
The program is finished with the finalisation of 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 and the closing of the try block:
 1.8.1.2
1.8.1.2