Table of Contents

Unsymmetric Matrices

For unsymmetric matrices, 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 implements LU and LDU factorisation, i.e. the matrix 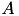$ A $ is factorised into

$A = LU \quad \textnormal{or} \quad A = LDU$

with a lower triangular, unit diagonal matrix 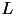$ L $ , a upper triangular matrix 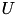$ U $ and, in the case of LDU a diagonal matrix 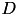$ D $ (in which case 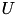$ U $ is also unit diagonal).

Both matrix factorisation are available in two modes:

block-wise: the matrix factorisation is performed up to leaf matrices in the matrix hierarchy, e.g. dense diagonal matrices are not factorised but inverted.
point-wise: a real LU (LDU) factorisation is computed, i.e. also dense diagonal blocks are factorised.

In the case of point-wise factorisation, the possibility of a break-down is high because pivoting is only possible to a very small degree for 𝓗-matrices and therefore not implemented in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈. Therefore, block-wise factorisation is the default factorisation mode, since it can only break down in the case of singular diagonal blocks (in which case some remedy is avaibable, see below).

The factorisation methods are implemented in the classes TLU and TLDU. Factorising 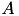$ A $ using default parameters can be performed as

TLU        fac;
TTruncAcc  acc( 1e-4 );
fac.factorise( 1, A, acc );

Here, one thread and a block-wise accuracy of 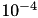$10^{-4}$ were used during LU. By replacing TLU with TLDU, the corresponding factorisation method is used. Furthermore, for both variants, functional forms are available, called lu and ldu:

TTruncAcc  acc( 1e-4 );
ldu( 1, A, acc );

Evaluation of Factorised Matrices

Matrix factorisation is performed in place, i.e. the individual factors are stored within 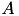$ A $ , thereby overwriting the original content. That also means, that 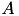$ A $ can no longer be used as a standard matrix object, e.g. for matrix vector multiplication, since for that, the content needs special interpretation, e.g. first multiply with upper triangular part, then with lower triangular.

Special classes are avaiable in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 to perform such interpretation, namely:

TLUMatrix, TLDUMatrix: compute matrix vector product 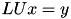and 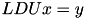respectively,
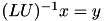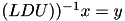TLUInvMatrix, TLDUInvMatrix: compute matrix vector product $(LU)^{-1} x = y$ and $(LDU))^{-1} x = y$ respectively.

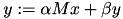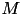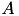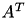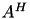All matrix vector products are available in the general form $y := \alpha M x + \beta y$ where $ M $ is either $ A $ , $ A^T $ or $ A^H $ (see ???).

Remarks: Since the "Inv" classes provide evaluation of the inverse, they can be used for preconditioning while solving equation systems iteratively (see ???).

TLUMatrix (TLDUMatrix) and TLUInvMatrix (TLDUInvMatrix) objects may be created explicitely or by using the corresponding functions of TLU (TLDU):

autoptr< TMatrix >  A_fac( fac.eval_matrix( A ) ); // return TLUMatrix/TLDUMatrix
autoptr< TMatrix >  A_inv( fac.inv_matrix( A ) );  // return TLUInvMatrix/TLDUInvMatrix
autoptr< TVector >  x = ... // set up some vector
autoptr< TVector >  y = ... // set up some vector
// eval A x = y
A_fac->mul_vec( 1.0, x.get(), 0.0, y.get(), MATOP_NORM );
// eval A^-1 x = y
A_inv->mul_vec( 1.0, x.get(), 0.0, y.get(), MATOP_TRANS );

Factorisation Parameters

So far, matrix factorisation was performed with default parameters. Options for matrix factorisation are provided in the form of a fac_options_t object. With it, you may select point-wise factorisation, e.g.:

fac_options_t  facopt;
facopt.eval = point_wise;
TLU  fac( facopt );

Also, a progress meter may be assigned for the factorisation:

TStreamProgressBar  progress( cout );
facopt.progress = & progress;

Furthermore, special modifications in case of a factorisation failure, e.g. for a singular matrix or for a matrix with a bad condition, may be activated.

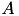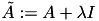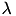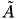add_identity: replace by $\tilde A := A + \lambda I$ , with $\lambda$ being chosen in some interval $[\lambda_0,\lambda_1]$ until $\tilde A$ can be factorised,
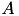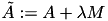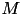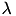add_random: replace by $\tilde A := A + \lambda M$ , with a random matrix and $\lambda$ as in the previous case,
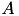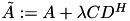add_random_lr: replace by $\tilde A := A + \lambda C D^H$ , with a random low-rank matrices 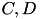with increasing rank until a successfull factorisation can be computed ( 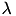$\lambda$ as before),
fix_cond: if 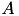has a very high condition, its singular values 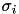$\sigma_i$ will be shifted by 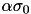$\alpha \sigma_0$ , e.g. the largest singular value.

The first three modification techniques are exclusive, i.e. may not be combined, whereas the last method can be used parallel to the others. Furthermore, all modifications only apply to dense diagonal blocks, thereby bounding the computation complexity of all methods such that the overhead can be neglected.

facopt.add_identity = true;

facopt.fix_cond = true;

Remarks: In most applications, using add_identity (combined with fix_cond) is best for handling errors during factorisation.

Symmetric/Hermitian Matrices

If 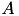$ A $ is symmetric ( 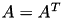$ A = A^T $ ) or hermitian ( 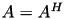$ A = A^H $ ), 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 provides the Cholesky (LL) and the LDL factorisation. These are implemented in the classes TLL and TLDL:

TLDL       fac;
TTruncAcc  acc( 1e-4 );
fac.factorise( 1, A, acc );

or available in functional form:

TTruncAcc  acc( 1e-4 );
ll( 1, A, acc );

Remarks: Please note, that TLU and TLDU will not work for symmetric/hermitian matrices as only the lower triangular part is stored and therefore, will throw an exception if called with such a matrix.

Again, all factorisation is performed in place and for further evaluation, special matrix objects are needed. Evaluation of 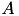$ A $ is provided by TLLMatrix and TLDLMatrix, whereas evaluation of 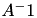$ A^-1 $ is implemented in TLLInvMatrix and TLDLInvMatrix. Please note, that the matrix format, e.g. whether symmetric or hermitian, is lost during factorisation but crucial for matrix evaluation and therefore, has to be provided while constructing these matrix objects:

TLDL             fac;
TTruncAcc        acc( 1e-4 );
const matform_t  matform = A->form()
fac.factorise( 1, A, acc );
autoptr< TMatrix >  A_inv( fac.inv_matrix( A, matform ) );

TLDL uses block-wise factorisation but can be switched to point-wise mode using fac_options_t objects as described above. Also, factorisation modifications/stabilisations may be activated for LDL factorisation. Neither of these is supported for Cholesky factorisation as this always used point-wise mode (block-wise is not possible). It is therefore not as stable as LDL factorisation.