Table of contents

Matrix-Vector Multiplication

Matrix-vector multiplication in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 is provided in the form of a vector update:

$y := \alpha \cdot M \cdot x + \beta y$

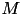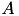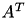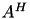Here, $ M $ is either $ A $ , $ A^T $ or $ A^H $ for a given matrix 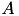$ A $ . The individual form of 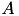$ A $ is specified by a value of type matop_t:

MATOP_NORM: ,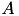
MATOP_TRANS: ,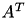
MATOP_CONJ: .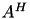

Remarks: Since 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 is based on BLAS/LAPACK, using just the conjugate of a matrix, e.g. 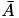$\bar A$ , is not supported.

Each matrix classes provides the method mul_vec for real and cmul_vec for complex valued factors $\alpha,\beta$ (see TMatrix), which perform the corresponding operations:

autoptr< TVector >  x( ... ); // define some vector
autoptr< TVector >  y( ... ); // define some vector
autoptr< TMatrix >  A( ... ); // define some matrix
A->mul_vec( 1.0, x.get(), 0.0, y.get(), MATOP_NORM );
A->mul_vec( complex( -2.0, 0.5 ), x.get(), complex( 1.0, 4.0 ), y.get(), MATOP_CONJ );

Additionally, the function mul_vec is available, which also handles the case of a distributed matrix (on distributed memory). To use it, the header file algebra/mul_vec.hh has to be included.

Matrix Addition

After including algebra/mat_add.hh into the corresponding source file, the function add is available for matrix addition. It implements the matrix update

$C := \alpha \cdot A + \beta \cdot C$

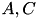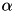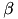with matrices $ A, C $ . Here, $\alpha$ and $\beta$ are real valued. For the complex valued case, the corresponding function is called cadd:

autoptr< TMatrix >  A( ... ); // define some matrix
autoptr< TMatrix >  C( ... ); // define some matrix
TTruncAcc           acc( 1e-6 );
add(  mach_info.nthreads(), 2.0,                  A.get(), 
                           -1.0,                  C.get(), acc );
cadd( mach_info.nthreads(), complex( -0.5, 2.0 ), A.get(), 
                            complex( 0.0, -1.0 ), C.get(), acc );

Matrix addition supports multi threaded execution, hence the first argument of both functions defines the number of threads to use.

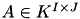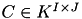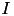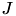A crucial requirement for the matrix addition as well as for all matrix operations, is the compatibility of the corresponding index sets and cluster trees, i.e. if $A \in K^{I \times J}$ then also $C \in K^{I \times J}$ must hold and the cluster trees for $ I $ and $ J $ have to be equal for both matrices. Only the block cluster trees may differ, e.g. a different admissibility condition can be used for both matrices.

A special for of matrix addition is implemented in add_identity (cadd_identity), in which

$A := A + \lambda I$

is implemented:

add_identity( A.get(), 2.0 );

Currently, this is only implemented if 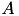$ A $ has dense diagonal blocks, e.g. which is th case for standard admissibility. Furthermore, since the operation only affects the diagonal part, it is an exact addition without truncation.

Matrix Multiplication

General matrix multiplication is provided by the module mat_mul, e.g. you have to include