Problem Description

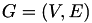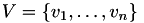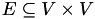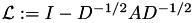Given is a Graph $G = (V,E)$ with nodes $V = \left\{v_1,\ldots,v_n\right\}$ and edges $E \subseteq V \times V$ . Let $\mathcal{L} := I - D^{-1/2} A D^{-1/2}$ be the normalised Laplacian of 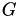$G$ with diagonal 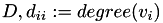$D, d_{ii} := \mathnormal{degree}(v_i)$ , and adjacency matrix $A$ ,

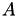$a_{ij} := \left\{ \begin{array}{ll} 1 & (i,j) \in E \\ 0 & \textnormal{otherwise} \end{array} . \right.$

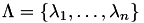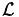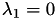We are looking for the spectrum $\Lambda = \left\{ \lambda_1, \ldots, \lambda_n \right\}$ of $\mathcal{L}$ . Please note, that $\Lambda \subset [0,2]$ with $\lambda_1 = 0$ .

Computing all eigenvalues 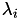$\lambda_i$ is usually extremly costly. However, sometimes not the exact spectrum is of interest but the general distribution of eigenvalues, which permits to characterise certain properties of matrices and especially graphs.

Applying the convolution

$f_{\mu}(\lambda_0) := \sum_{\lambda_i} \int k_{\mu}(\lambda_0,\lambda') \delta(\lambda' - \lambda_i) d\lambda'$

with

$k_{\mu}(\lambda_0,\lambda') := \frac{\mu}{(\lambda' - \lambda_0)^2 + \mu^2}$

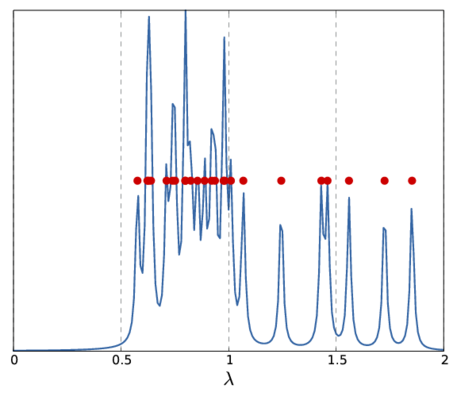
and 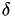$\delta$ being the usual delta distribution, one obtains a graphical representation of the spectrum. An example for this is shown in the following picture for a small graph (left) and the convoluted spectrum of its Laplacian together with the eigenvalues.


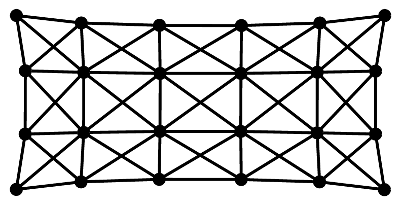
Graph	Spectrum

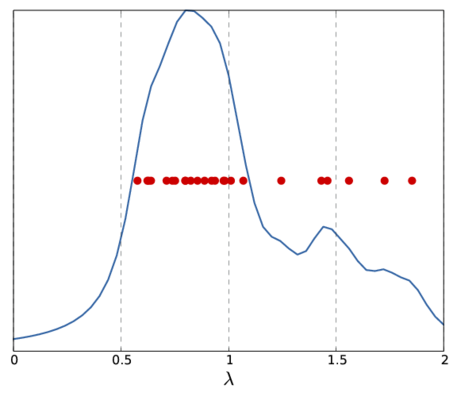
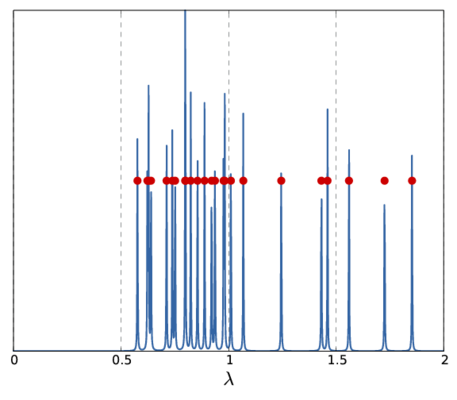
Note, that the above 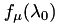$f_{\mu}(\lambda_0)$ only represents a single sample for the whole spectrum. Depending on the sample frequency and the choice of 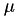$\mu$ , the final image shows more or less details of the spectrum. The following picture show two other versions of the above spectrum with a coarse (left) and fine (right) sampling.

Computation of the Spectrum

The above definition of 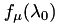$f_{\mu}(\lambda_0)$ contains the eigenvalues, which are not available. Hence, another way to compute 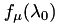$f_{\mu}(\lambda_0)$ is needed.

We start with the computation of the determinant of 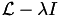$\mathcal{L}-\lambda I$ using LU factorisation. Since the determinant of triangular matrices is the product of their diagonal entries and since the diagonal entries of 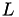$L$ are one, this can be restricted to the diagonal entries of $U$ :

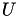$|\textnormal{det}(\mathcal{L}-\lambda I)| = |\textnormal{det}(LU)| = |\textnormal{det}(U)| = |\prod_i u_{ii}|.$

Applying the logarithm to both sides of the equation, we can change the product into a sum:

$\log |\textnormal{det}(\mathcal{L}-\lambda I)| = \log |\prod_i u_{ii}| = \sum_i \log |u_{ii}|.$

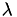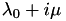Replacing $\lambda$ by $\lambda_0 + i\mu$ , one obtains

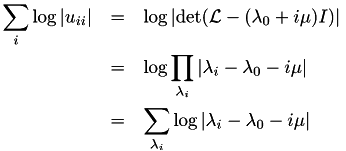
$\begin{eqnarray*} \sum_i \log |u_{ii}| & = & \log |\textnormal{det}(\mathcal{L}-(\lambda_0 + i\mu) I)| \\ & = & \log \prod_{\lambda_i} |\lambda_i - \lambda_0 - i\mu| \\ & = & \sum_{\lambda_i} \log |\lambda_i - \lambda_0 - i\mu| \end{eqnarray*}$

Here we have used the identity of the determinant with the corresponding characteristic polynomial 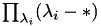$\prod_{\lambda_i} (\lambda_i - *)$ .

Finally, differentiation with respect to 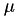$\mu$ yields

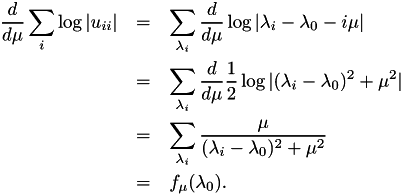
$\begin{eqnarray*} \frac{d}{d\mu} \sum_i \log |u_{ii}| & = & \sum_{\lambda_i} \frac{d}{d\mu} \log |\lambda_i - \lambda_0 - i\mu| \\ & = & \sum_{\lambda_i} \frac{d}{d\mu} \frac{1}{2} \log | (\lambda_i - \lambda_0)^2 + \mu^2| \\ & = & \sum_{\lambda_i} \frac{\mu}{(\lambda_i - \lambda_0)^2 + \mu^2} \\ & = & f_{\mu}(\lambda_0). \end{eqnarray*}$

Replacing the differentation by a (central) difference quotient makes the problem computable with a series of LU factorisations for 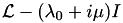$\mathcal{L}-(\lambda_0+i\mu)I$ for the different values of $\lambda_0$ . Furthermore, instead of an exact LU decomposition, the H-LU factorisation is used to obtain log-linear costs.

Sparse to ℋ-Matrix Conversion

The program starts by converting a sparse matrix, which is assumed to represent a graph laplacian, into an ℋ-matrix:

#include <iostream>
using namespace std;
using namespace HLIB;
int
main ( int      argc,
       char **  argv )
{
    std::string  matrixfile = "graph.mat";
    double       mu         = 1e-2;
    double       d          = 1e-3;
    uint         nsteps     = 100;
    double       eps        = 1e-4;
    try
    {
        HLIB::INIT();
        auto  M = read_matrix( matrixfile.c_str() );
        if ( ! IS_TYPE( M, TSparseMatrix ) )
        {
            std::cout << "input matrix is not sparse" << std::endl;
            return 1;
        }
        auto  S = ptrcast( M.get(), TSparseMatrix * );
        S->set_unsymmetric();
        TMETISAlgPartStrat  part_strat;
        TAlgCTBuilder       base_ct_builder( & part_strat, 100 );
        TAlgNDCTBuilder     nd_ct_builder( & base_ct_builder );
        auto                ct = nd_ct_builder.build( S );
        TWeakAlgAdmCond     adm_cond( S, ct->perm_i2e() );
        TBCBuilder          bct_builder;
        auto                bct = bct_builder.build( ct.get(), ct.get(), & adm_cond );
        TSparseMBuilder     h_builder( S, ct->perm_i2e(), ct->perm_e2i() );
        auto                L  = h_builder.build( bct->root(), acc_exact );

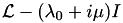In addition to $L$ also the identity matrix is needed to compute $\mathcal{L}-(\lambda_0+i\mu)I$ :

auto                Id = identity( bct.get() ); 
L->set_complex( true );
Id->set_complex( true );

Both matrices need to be complex valued since 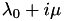$\lambda_0+i\mu$ is, except for 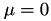$\mu = 0$ , which represents the limit case with exact representation of the spectrum.

Computing the Difference Quotient

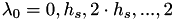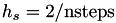For the computation of the spectrum in the sample space $[0,2]$ equally distant sample points are chosen as defined by the number of steps nsteps, i.e., $\lambda_0 = 0, h_s, 2 \cdot h_s, ..., 2$ with $h_s = 2/\textnormal{nsteps}$ .

Afterwards, for each value of 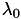$\lambda_0$ the difference quotient is computed and 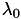$\lambda_0$ as well as the result of the difference quotient are stored:

const auto  lambda_0     = i * stepwidth;
const auto  f_mu_plus_h  = calc_abs_det( L, Id, lambda_0, mu+h, eps );
const auto  f_mu_minus_h = calc_abs_det( L, Id, lambda_0, mu-h, eps );
x(i) = lambda_0;
y(i) = (f_mu_plus_h - f_mu_minus_h) / (2 * h);

Since computation for different values of 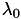$\lambda_0$ are independent, they may be computed in parallel. This is done by using the parallel_for algorithm from TBB:

tbb::parallel_for( uint(0), nsteps+1,
                   [=,&x,&y] ( const uint  i )
                   {
                      ...
                   } );

Remarks: Although H-LU scales very good with the number of cores, it is even more efficient to perform factorisations is parallel since there are still some portions of the algorithm implemented sequentially.

The result of the computation is stored in two objects of type BLAS::Vector and returned as a std::pair, which completes the function calc_y:

std::pair< BLAS::Vector< double >,
           BLAS::Vector< double > >
calc_y ( const TMatrix *  L,
         const TMatrix *  Id,
         const double     mu,
         const double     h,
         const uint       nsteps,
         const double     eps )
{
    BLAS::Vector< double >  x( nsteps+1 );
    BLAS::Vector< double >  y( nsteps+1 );
    const double            stepwidth = 2.0 / double(nsteps);
    tbb::parallel_for( uint(0), nsteps+1,
                       [=,&x,&y] ( const uint  i )
                       {
                           const auto  lambda_0     = i * stepwidth;
                           const auto  f_mu_plus_h  = calc_abs_det( L, Id, lambda_0, mu+h, eps );
                           const auto  f_mu_minus_h = calc_abs_det( L, Id, lambda_0, mu-h, eps );
                           x(i) = lambda_0;
                           y(i) = (f_mu_plus_h - f_mu_minus_h) / (2 * h);
                       } );
    return std::pair< BLAS::Vector< double >,
                      BLAS::Vector< double > >( std::move( x ),
                                                std::move( y ) );
}

This is then called from the main function via

auto spectrum = calc_y( L.get(), Id.get(), mu, d, nsteps, eps );

For visualization, both arrays are written to files in Matlab format, which finishes the program:

        TMatlabVectorIO  vio;
        vio.write( spectrum.first,  "x.mat", "x" );
        vio.write( spectrum.second, "y.mat", "y" );
        HLIB::DONE();
    }
    catch ( std::exception & e )
    {
        std::cout << e.what() << std::endl;
    }
}

Computing the Determinant

Left open is the computation of the determinant of 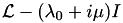$\mathcal{L}-(\lambda_0+i\mu)I$ implemented in calc_abs_det via ℋ-LU factorisation.

Before the factorisation, the matrix first has to be computed:

double
calc_abs_det ( const TMatrix *  L,
               const TMatrix *  Id,
               const double     lambda_0,
               const double     mu,
               const double     eps )
{
    auto           L_lmu_Id = L->copy();
    add( HLIB::complex( -lambda_0, -mu ), Id, HLIB::complex( 1, 0 ), L_lmu_Id.get(), acc_exact );

By default, 𝖧𝖫𝖨𝖡𝗉𝗋𝗈 uses block-wise LU factorisation, i.e., computes the inverse of diagonal blocks. In this case however, the point-wise LU factorisation is needed since the diagonal entries are used.

fac_options_t  opts;
opts.eval = point_wise;
factorise( L_lmu_Id.get(), fixed_prec( eps ), opts );

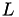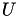After the factorisation, these diagonal entries only need to be extracted from the matrix. Note, that L_lmu_id stores $L$ and $U$ but since the diagonal entries of 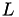$L$ are one and therefore not explicitly stored, the diagonal of L_lmu_id is equal to the diagonal of 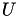$U$ .

To obtain the diagonal entries the function diagonal is available, which returns a vector containing the coefficients.

In order to prevent stability issues, the function tests for very small values and aborts further computation if such values are present:

    auto    diag = diagonal( L_lmu_Id.get() );
    double  sum  = 0.0;
    for ( auto  i : diag->is() )
    {
        const auto  u_ii     = diag->centry( i );
        const auto  norm_uii = std::sqrt( norm( u_ii ) );
        if ( norm_uii < 1e-12 )
        {
            std::cout << "detected near zero entry" << std::endl;
            return 0;
        }
        else
            sum += std::log( norm_uii );
    }
    return sum;
}

The Plain Program

#include <iostream>
#include <tbb/parallel_for.h>
#include "hlib.hh"
using namespace std;
using namespace HLIB;
double
calc_abs_det ( const TMatrix *  L,
               const TMatrix *  Id,
               const double     lambda_0,
               const double     mu,
               const double     eps )
{
    auto           L_lmu_Id = L->copy();
    fac_options_t  opts;
    opts.eval = point_wise;
    add( HLIB::complex( -lambda_0, -mu ), Id, HLIB::complex( 1, 0 ), L_lmu_Id.get(), acc_exact );
    factorise( L_lmu_Id.get(), fixed_prec( eps ), opts );
    auto    diag = diagonal( L_lmu_Id.get() );
    double  sum  = 0.0;
    for ( auto  i : diag->is() )
    {
        const auto  u_ii     = diag->centry( i );
        const auto  norm_uii = std::sqrt( norm( u_ii ) );
        if ( norm_uii < 1e-12 )
        {
            std::cout << "detected near zero entry" << std::endl;
            return 0;
        }
        else
            sum += std::log( norm_uii );
    }
    return sum;
}
std::pair< BLAS::Vector< double >,
           BLAS::Vector< double > >
calc_y ( const TMatrix *  L,
         const TMatrix *  Id,
         const double     mu,
         const double     d,
         const uint       nsteps,
         const double     eps )
{
    BLAS::Vector< double >  x( nsteps+1 );
    BLAS::Vector< double >  y( nsteps+1 );
    const double            stepwidth = 2.0 / double(nsteps);
    tbb::parallel_for( uint(0), nsteps+1,
                       [=,&x,&y] ( const uint  i )
                       {
                           const auto  lambda_0     = i * stepwidth;
                           const auto  f_mu_plus_d  = calc_abs_det( L, Id, lambda_0, mu+d, eps );
                           const auto  f_mu_minus_d = calc_abs_det( L, Id, lambda_0, mu-d, eps );
                           x(i) = lambda_0;
                           y(i) = (f_mu_plus_d - f_mu_minus_d) / (2 * d);
                       } );
    return std::pair< BLAS::Vector< double >,
                      BLAS::Vector< double > >( std::move( x ),
                                                std::move( y ) );
}
int
main ( int      argc,
       char **  argv )
{
    std::string  matrixfile = "graph.mat";
    double       mu         = 1e-2;
    double       h          = 1e-3;
    uint         nsteps     = 100;
    double       eps        = 1e-4;
    try
    {
        HLIB::INIT();
        auto  M = read_matrix( matrixfile.c_str() );
        if ( ! IS_TYPE( M, TSparseMatrix ) )
        {
            std::cout << "input matrix is not sparse" << std::endl;
            return 1;
        }
        auto  S = ptrcast( M.get(), TSparseMatrix * );
        S->set_unsymmetric();
        TMETISAlgPartStrat  part_strat;
        TAlgCTBuilder       base_ct_builder( & part_strat, 100 );
        TAlgNDCTBuilder     nd_ct_builder( & base_ct_builder );
        auto                ct = nd_ct_builder.build( S );
        TWeakAlgAdmCond     adm_cond( S, ct->perm_i2e() );
        TBCBuilder          bct_builder;
        auto                bct = bct_builder.build( ct.get(), ct.get(), & adm_cond );
        TSparseMBuilder     h_builder( S, ct->perm_i2e(), ct->perm_e2i() );
        auto                L  = h_builder.build( bct->root(), acc_exact );
        auto                Id = identity( bct.get() ); 
        L->set_complex( true );
        Id->set_complex( true );
        auto  spectrum  = calc_y( L.get(), Id.get(), mu, h, nsteps, eps );
        TMatlabVectorIO  vio;
        vio.write( spectrum.first,  "x.mat", "x" );
        vio.write( spectrum.second, "y.mat", "y" );
        HLIB::DONE();
    }
    catch ( std::exception & e )
    {
        std::cout << e.what() << std::endl;
    }
}

Example Matrices

The Sparse Matrix Collection from the University of Florida provides a wide range of sparse matrices.

The following Matlab function will compute the normalised Laplacian from a given sparse matrix, assuming the matrix contains the adjacency matrix of the graph (loops are ignored!).

function [ Ln ] = laplacian ( A )
  s    = size(A);
  n    = s(1);
  sums = sum( A );
  D=sparse([1:n],[1:n],sums,n,n);
  L=tril(A,-1)+D+triu(A,1);
  invsums = 1./sqrt(sums);
  D=sparse([1:n],[1:n],invsums,n,n);
  Ln = D*L*D;
end

Table of Contents