Table of Contents
The foundation of HLIBpro is provided by the BLAS and LAPACK software packages. Especially the advanced functions of LAPACK, e.g. singular value decomposition, play a crucial role in the H-arithmetics. To simplify the usage of these functions and to reduce the potential for errors, an extra layer was implemented between the H-arithmetics and the BLAS/LAPACK functions. The BLAS module provides this layer.
All data classes in the BLAS namespace share special properties with respect to the memory management of the underlying data:
- Each class is implemented as a template with the base datatype as the template parameter, e.g. double or complex.
- Data is not necessarily contiguous inside a memory block, e.g. you may address each second element of a memory block. This is especially needed to address sub matrices, where each column starts with a certain offset with respect to the previous column.
- You may not change the size of a vector or matrix, only assigning a vector or matrix of a different size.
- In contrast to H-matrices and vectors, indices for BLAS vectors and matrices always start at 0.
Since the matrix and vector classes were implemented with BLAS/LAPACK in mind, some restrictions apply:
- All data is stored column-wise.
- No mix of datatypes is possible, e.g. multiplying double and complex matrices.
For the following code, an
is assumed.
Memory Management
Due to performance issues on multi-core systems the memory management of the BLAS classes was changed in HLIBpro. Please read the following carefully to prevent programming errors.
Both vector and matrix classes in the BLAS namespace store a pointer to some memory block. This memory may be either owned or referenced by the corresponding object. If the pointer only references some memory block owned by another object, no reference counting is done. Hence, if the owning object is freed, the reference will be invalid.
A major cause of such problems are temporary objects, e.g. some auxilliary vectors or matrices inside a function, which are assigned to some return value:
Here, x will by default only reference t. To make the new owner of the data in t, one has to use the move semantics in C++:
Now, t will be empty and x owns the data of t.
If the result is the return value of the function, the compiler will automatically choose the move semantics:
Ranges
A range is an index set in the BLAS namespace.
Here, an index set containing  is defined. Please note, that the index interval is closed on both ends, e.g. the first and the last index is given.
is defined. Please note, that the index interval is closed on both ends, e.g. the first and the last index is given.
In addition to a standard index set, you may also define a stride, e.g. a distance between elements in the index set:
This defines the index set 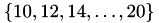
For convenience, a constructor for an index set containing just one element is also available:
yields 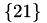 .
.
Furthermore, the special range Range::all indicates, that the whole range shall be used:
Here, all columns of M are used in M2 but only the rows 5 to 10.
Vectors
Construction
Usually, a BLAS vector is intialised with the corresponding size as the constructor argument:
creates a double vector of size 10. Leaving out the size argument, intialises the vector with size 0:
Providing another vector in the constructor, creates a new vector pointing to the same data as the argument vector:
Changing z also changes x!
With the usage of range objects, parts of vectors can be represented as another vector:
Here, x2 addresses the second half of the coefficients of x1 whereas x3 contains each second coefficient of x2 and by that, the coefficients 5, 7 and 9 of x1.
By default, the policy for the copy constructors is to use a reference to the given data. You may change that, such that a copy of the data is created, e.g. a new memory block is allocated:
Now, x3 does not address any coefficients in x1 or x2.
Accessing Coefficients and Vector Properties
Single coefficients in vectors are accessed using the () operator:
The length of a vector is accessible via the length() function:
Algebra
Most of the BLAS vector functions are available in HLIBpro and some, which have no representation in the BLAS package.
An examples, involving filling, scaling vectors, forming linear combinations and computing dot products:
As mentioned before, you can not mix vectors of different value type, e.g.
since BLAS/LAPACK do not support such mixing
For a complete overview of the algebra functions refer to the BLAS module.
Matrices
Construction
Constructing matrices follows the same scheme as vectors, with the only difference being the additional dimension:
Addressing subblocks of a given matrix is done by providing Range objects:
Here, M2 references the last 10 rows of M1. M3 also shares these coefficients but further restricts the elements to each second column of M1. Hence
will affect the same memory position.
- Remarks
- This also introduces the coefficient access for matrices, again being the standard index operator.
The standard copy policy for matrices, i.e. copy_reference, can be changed by the last, optional parameter to the above constructor:
This will create a 10×10 matrix with coefficients copied from matrix M2.
Algebra
As for vectors, the arithmetic functionality is implemented as functions and not as special C++ operators for objects of type Matrix.
Matrix views
𝖧𝖫𝖨𝖡𝗉𝗋𝗈 provides different <emph>matrix view</emph> for accessing matrices, e.g. transposed and hermitian view. A view object will not change or copy the data of a matrix but changes for instance the way the data is access, e.g. interchanging the indices. For a given matrix
The transposed view of M is defined by
and the adjoint view by
These views may be used for arithmetic functions, albeit not all functions, to simplify the usage and to enhance the performance of these functions.
Matrix-Vector Arithmetic
The most common form of matrix-vector arithmetic is the matrix vector multiplication in the general form
![\[ y := \alpha A x + \beta y \]](form_235.png)
:
Using matrix views allows the multiplication with the transposed or adjoint matrix:
If M is a triangular matrix, the multiplication is performed in place, i.e. the single argument vector is modified:
![\[ x := A \cdot x \]](form_236.png)
The exact shape of the matrix is defined by additional arguments of type tri_type_t (lower_triangular or upper_triangular) and diag_type_t (unit_diag or general_diag). The second argument describes the diagonal which is either identical to 1 or not:
- Remarks
- The shape of the matrix, e.g. lower or upper triangular, always refers to the original matrix and not the provided view!
Also available is the rank-1 update of a matrix
![\[ A := A + \alpha a \cdot b^H \]](form_237.png)
:
For triangular matrices  , solving equation systems
, solving equation systems 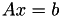 is supported via:
is supported via:
Here, upon input x contains 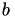 b and is overwritten with the result
b and is overwritten with the result 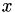 .
.
Matrix-Matrix Arithmetic
The BLAS namespace defines common functions for single matrices and between matrices. Single matrix functions are
- Remarks
- PLease note, that the last two functions will only work for square matrices!
Different matrix norms are available:
Other functions, involving more matrices are:
Inversion and factorisation functions are:
- Remarks
- All factorisation functions are without pivoting!
It is also possible to solve matrix equations of the form
![\[ A X = B \]](form_239.png)
with known 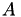 and
and 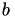 :
:
X will initially contain the matrix 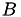 . Furthermore, the content of the matrix
. Furthermore, the content of the matrix A will be destroyed during computation.
If 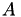 is a triangular matrix, the equation may take the more general forms:
is a triangular matrix, the equation may take the more general forms:
![\[ A X = \alpha B \quad \textnormal{or} \quad X A = \alpha B \]](form_240.png)
The corresponding side from which to apply 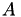 to
to 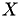 is defined by a parameter (
is defined by a parameter (form_left or form_right):
Eigenvalues and singular values and vectors of a matrix can also be computed:
If M is symmetric, selected eigen values may be computed:
